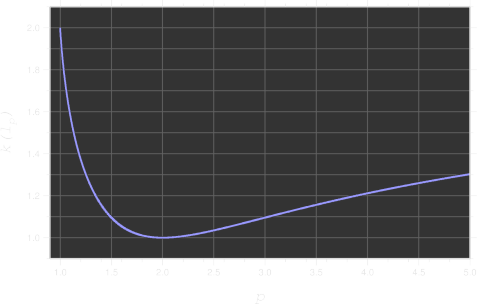
La projection radiale, $\rho$, sur un espace normé $X$ est la fonction (non linéaire) donné par $$ \rho(x) = \begin{cases} x/\left\|x\right\| & \text{pour $\left\|x\right\| \geq 1$} \\ x & \text{sinon.} \end{cases} $$ La constante de Lipschitz pour cette fonction est the plus petite $k$ pour lequelle $$ \left\| \rho(x) - \rho(y) \right| \leq k \left\| x-y \right\| \qquad (x,\,y\in X). $$ Ceci est une quantité d’intérêt dans la géométrie des espaces vectoriels normés et des espaces de Banach. Franchetti a montré que la constante de Lipschitz, pour $X$ l’espace de dimension finie $\ell^2_p(\R)$ ou l’espace des fonctions $L^p[0,1]$, est donné par le maximum d’une fonction $p$-dépendante à une dimension. L’isometries bien connus $$ \ell^2_p(\R) \subseteq \ell^3_p(\R) \subseteq \cdots \subseteq \ell_p(\R) \subseteq L^p[0,1] $$ implique que la même chose est vraie pour les espaces de dimension finie $\ell^n_p(\R)$ ($n=2,3,\ldots$) et pour l’espace des séquences $\ell_p(\R)$. Ce dernier dispose d’une application dans le calcul efficace de $(p,q)$-opérateur norme de matrices, c’est à dire, la norme d’une matrice considéré comme un opérateur $\ell_p\rightarrow\ell_q$. Voir, par example, le progiciel opnorm.

Ci-dessous nous fournissons quelques codes d’évaluer efficacement cette constante de Lipschitz.

• lcrp.m pour Octave/Matlab
• le realisation en C99/C++ et son manuel
• une note technique sur les aspects numériques de la méthode de calcul.