All integrable Hamiltonian systems are alike, while each nonintegrable one is nonintegrable in its own way
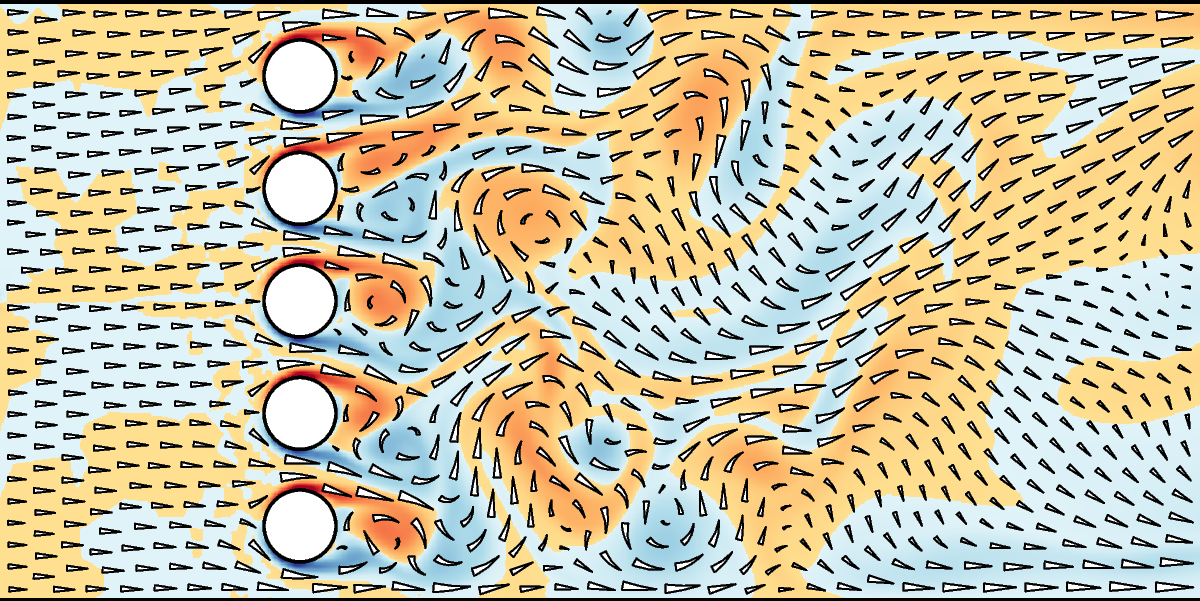
flow through a coarse grating
G I Taylor, E G Richardson and G K Batchelor used gratings in wind-tunnels in much of their early experimental work on turbulence.
Here a coarse two-dimensional grating in a pipe is modeled with Gerris, the GFS output of the simulation at 2 seconds converted to GMT grd files and the arrows layer generated with
vfplot \
--verbose \
--width 8in \
--margin 5/5/-0.4 \
--scale 3e-4 \
--iterations 500/5 \
--pen 0.25mm \
--fill 255 \
--length 0/1in \
--cache 256 \
--aspect 4.0 \
--symbol triangle \
--output vfplot.eps \
grd/u.grd grd/v.grd